课题组日志
基于小波神经网络和马尔可夫链的高速公路行程时间预测方法
作者:杨航
发布时间:2016-03-17
1、阿尔法狗与神经网络
(1)介绍阿尔法狗(AlphaGo)的构成以及涉及的大致程序原理
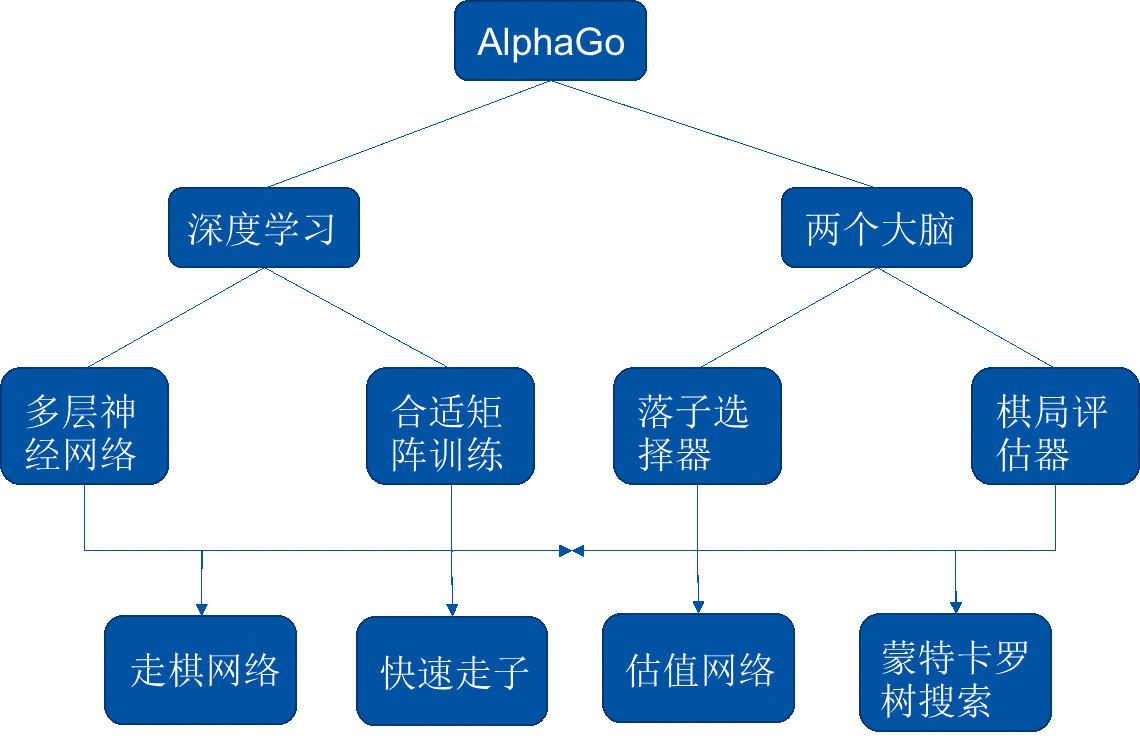
(2)阐述快速走子与走棋网络的区别,引出神经网络与平稳随机过程结合的必要性
a、快速走子运行速度是走棋网络的1000倍
b、单纯神经网络易出现震荡,且收敛速度慢
c、结合传统局部特征匹配法可使最速下降法实现自动调参
2、引言
(1)高速公路行程时间预测的必要性
a、道路交通状态的重要评价指标
b、实现ITS系统中多项重要功能的前提条件
c、为动态交通管理决策和出行决策提供基础数据
(2)国内外研究情况的文献综述
(3)现有阶段研究的局限性
a、较多单纯考虑统计模型或者人工智能模型,较少探究二者结合之后的预测精度
b、对于预测中的时空因素考虑不多,涉及的研究较少
c、使用马尔可夫过程进行预测时采用的是对拥堵状态进行状态打分,存在一定的主观性
(4)本研究需要完成的内容
a、改进传统小波神经网络模型,使得模型具备动态决定隐藏层节点数的能力
b、对相对误差进行状态划分,降低状态等级划分的主观性
c、融合小波神经网络与马尔可夫链,产生混合预测模型
d、考虑预测中的时空信息,提高相邻路段行程时间的预测精度
3、行程时间数据
(1)数据来源
美国,德克萨斯州,休斯顿,US-290中I-610至FM-1960段,2008.01-2008.08
(2)数据采集设备
AVI
(3)数据采集间隔
五分钟
(4)各路段行程时间的周期性和时空性分析
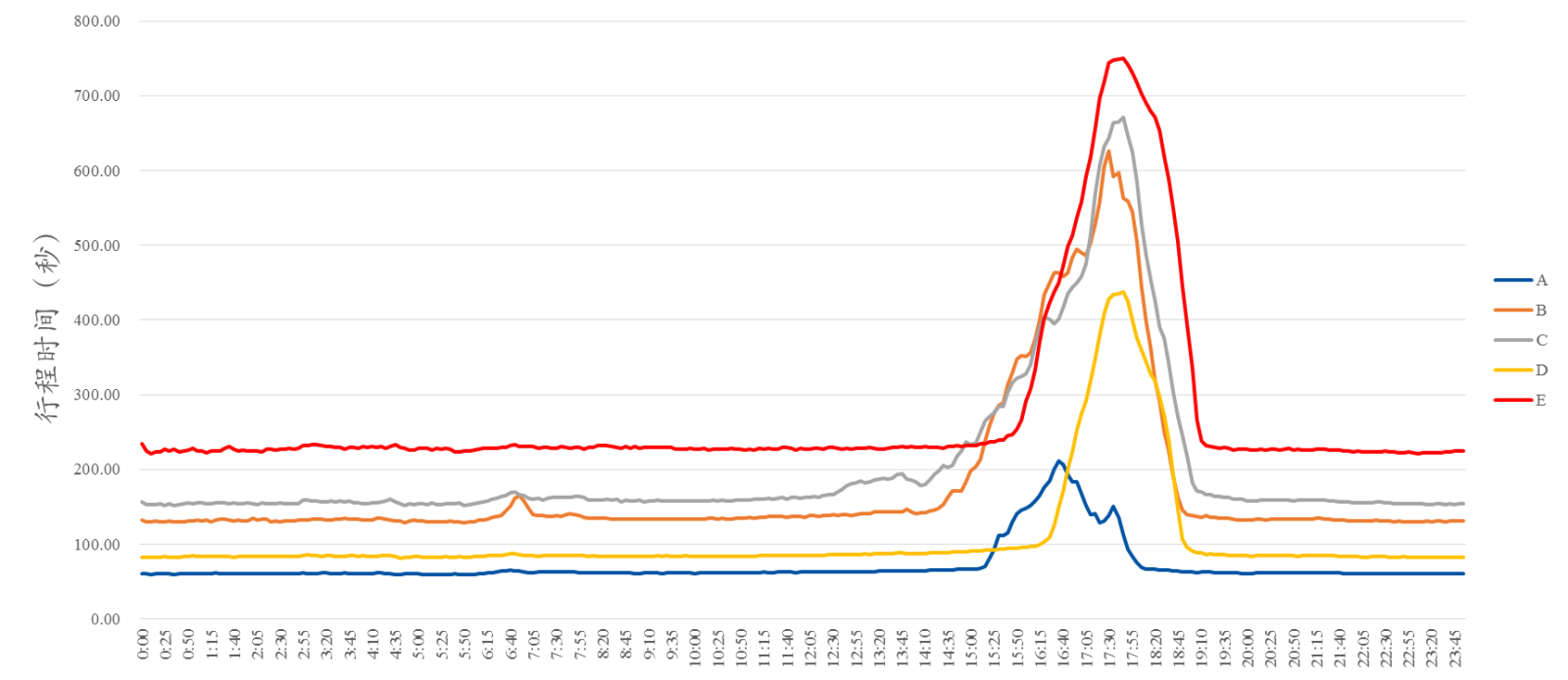
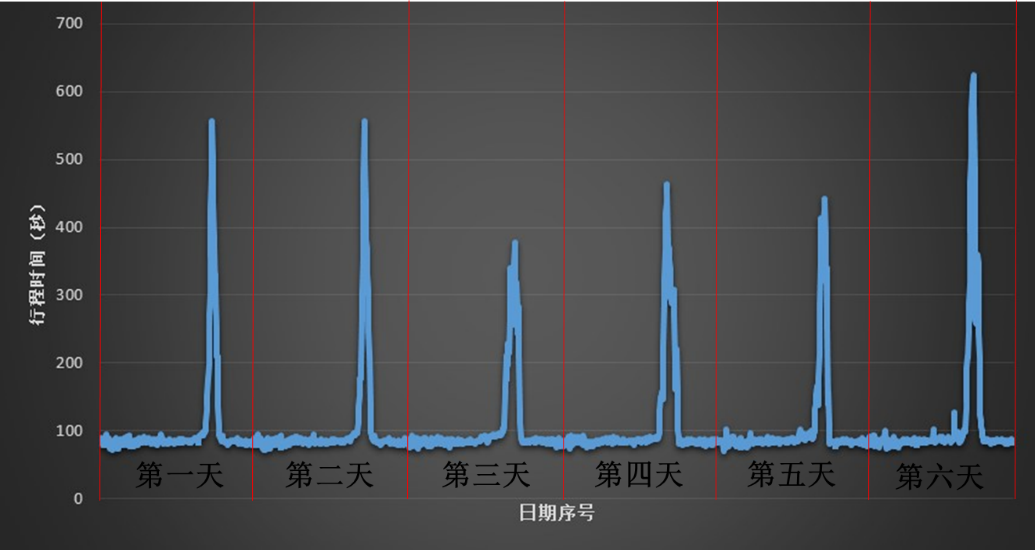
4、混合模型
(1)小波理论
针对傅里叶变换在时域中没有分辨能力的缺点发展而来,特点包括:时域都具有紧支集或近似紧支集以及直流分量为0。
小波基函数:
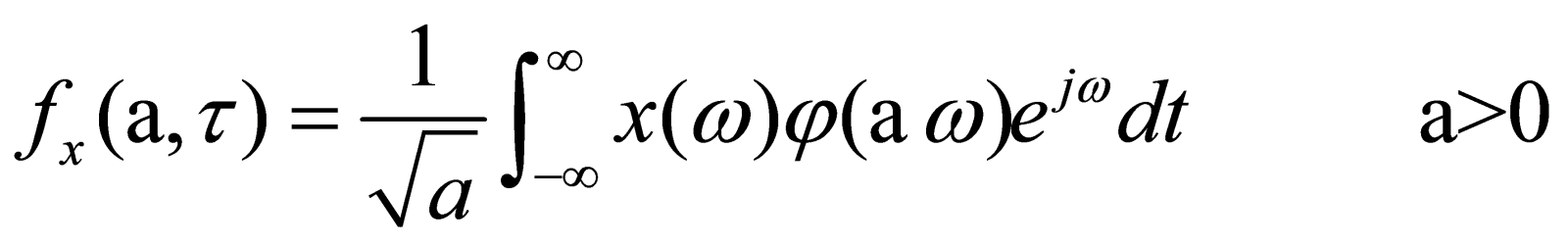
(2)小波神经网络
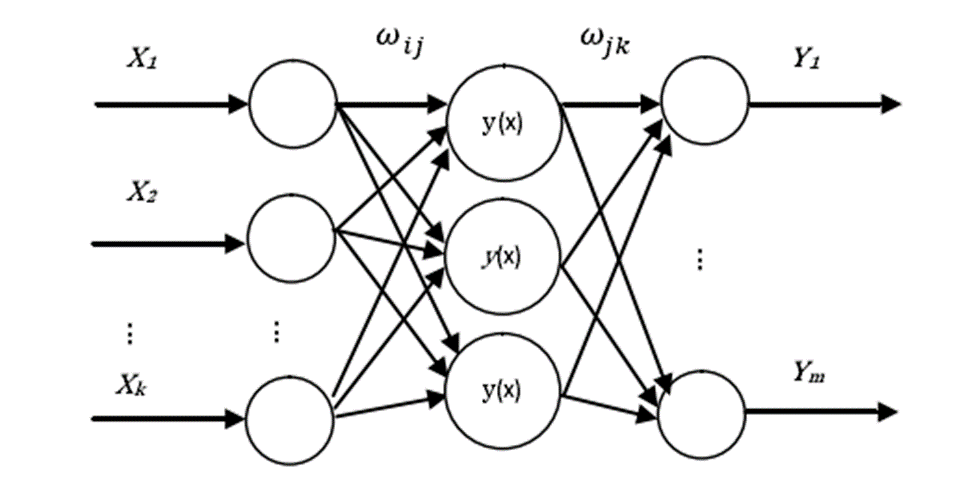
(3)马尔可夫链(MKC)
状态划分:

根据历史误差状态集建立一步概率转移矩阵,并根据初始状态矩阵求得最终误差状态矩阵。
(4)混合模型建立
由小波神经网络求得初始行程时间预测值,再由马尔可夫链对预测残差就行修正,两者相结合得到最终的预测混合模型。
5、各模型精度比较
BP、小波、AR(2)、BP+MKC、小波+MKC、AR(2)+MKC六种模型的精度比较
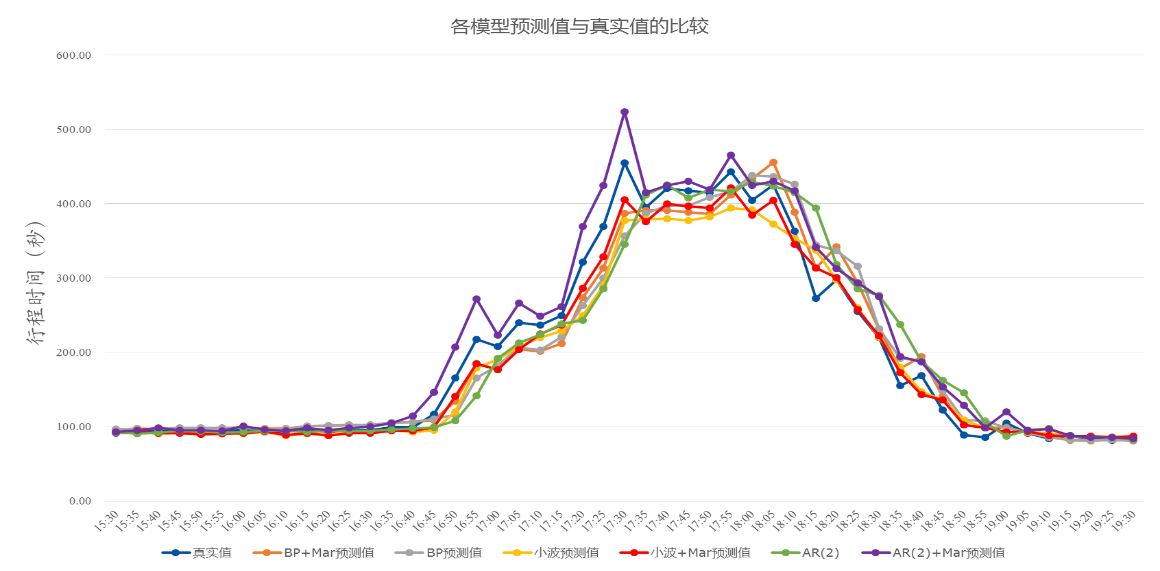
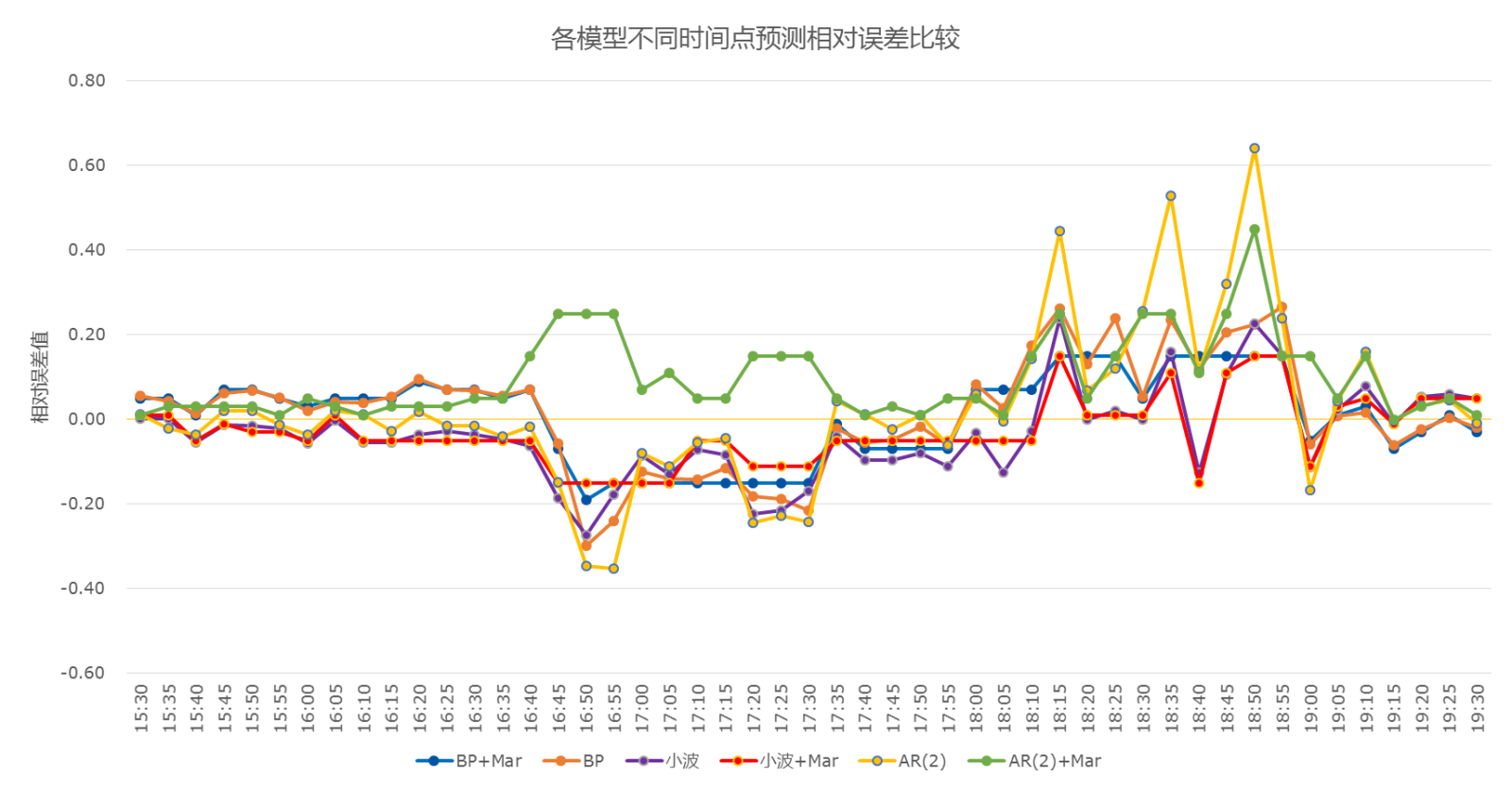
6、结论
(1)六种模型中小波+MKC预测精度最高
(2)马尔可夫链对BP、小波和AR(2)都有预测精度提高的作用
(3)在混合模型中,马尔可夫链对于结构相对简单的AR(2)模型的精度提升幅度最大
(4)小波+MKC的混合模型对于异常交通状况下的行程时间拐点具有较强的拟合性和提前预知性